Hoe Werkt De Stelling Van Pythagoras In De Praktijk?
Hoedoeje: Hoe Werkt De Stelling Van Pythagoras
Keywords searched by users: hoe werkt stelling van pythagoras stelling van pythagoras voorbeeld, stelling van pythagoras hoek berekenen, hoe werkt de stelling van pythagoras, stelling van pythagoras calculator, stelling van pythagoras met 2 onbekenden, stelling van pythagoras online, omgekeerde stelling van pythagoras, toepassingen stelling van pythagoras
Wat is de stelling van Pythagoras?
De stelling van Pythagoras is een fundamenteel concept in de wiskunde dat het verband legt tussen de lengtes van de zijden van een rechthoekige driehoek. Volgens deze stelling is het kwadraat van de lengte van de schuine zijde (de zijde tegenover de rechte hoek) gelijk aan de som van de kwadraten van de lengtes van de andere twee zijden.
De stelling kan worden uitgedrukt in een formule: a² + b² = c². Hierbij staat a voor de lengte van de ene rechthoekszijde, b voor de lengte van de andere rechthoekszijde en c voor de lengte van de schuine zijde.
De stelling van Pythagoras kan worden toegepast op elke rechthoekige driehoek, ongeacht de grootte of verhouding van de zijden. Het biedt een basis voor het berekenen van ontbrekende lengtes of het controleren van de juistheid van een driehoek.
De formule van de stelling van Pythagoras
De formule van de stelling van Pythagoras is als volgt: a² + b² = c². Hierbij zijn a en b de lengtes van de rechthoekszijden en c de lengte van de schuine zijde.
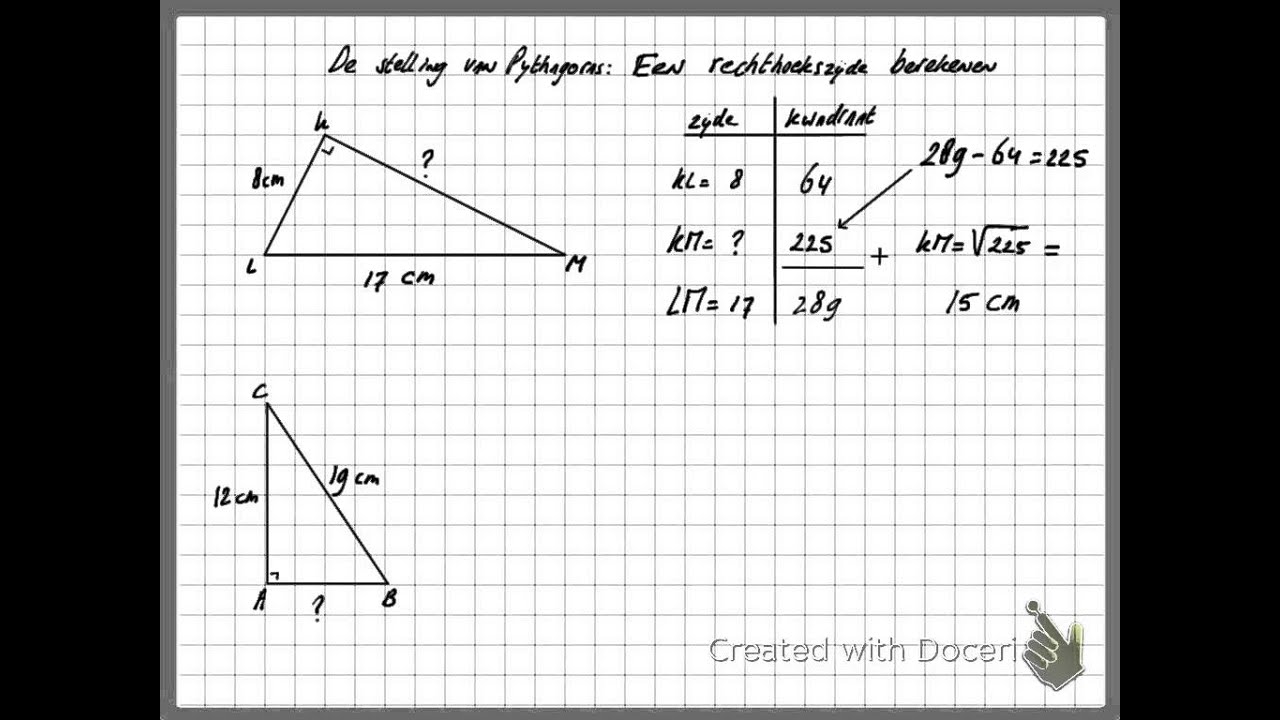
Om de lengte van een zijde te bepalen, kunnen we de formule herleiden naar: a = √(c² – b²) en b = √(c² – a²). Dit stelt ons in staat om de ontbrekende zijde te berekenen als we de lengtes van de andere twee zijden kennen.
Werken met rechthoekige driehoeken
Om de stelling van Pythagoras toe te passen, moeten we eerst bevestigen dat de driehoek rechthoekig is. Dit kunnen we doen door te controleren of één van de hoeken 90 graden is.
Als we alle zijden van de driehoek kennen, kunnen we de stelling gebruiken om de juistheid ervan te controleren. We berekenen het kwadraat van beide rechthoekszijden en tellen deze op. Vervolgens berekenen we het kwadraat van de schuine zijde. Als beide waarden gelijk zijn, dan is de driehoek rechthoekig en geldt de stelling van Pythagoras.
Als we eenmaal weten dat de driehoek rechthoekig is, kunnen we de stelling gebruiken om ontbrekende zijden te berekenen. Door de bekende zijden in te vullen in de formule, kunnen we de ontbrekende zijde vinden. Dit is vooral handig bij het oplossen van meetkundige vraagstukken of het bepalen van afstanden in de ruimte.
Hoe bewijs je de stelling van Pythagoras?
Er zijn verschillende methoden om de stelling van Pythagoras te bewijzen. Een van de bekendste is het visuele bewijs, dat vaak wordt aangeduid als het “vierkantenbewijs”. Het idee achter dit bewijs is om vierkanten te construeren op elke zijde van de driehoek en vervolgens te laten zien dat de som van de oppervlaktes van de twee kleinere vierkanten gelijk is aan de oppervlakte van het grootste vierkant.
Een ander bewijs is het algebraïsche bewijs, waarbij gebruik wordt gemaakt van algebraïsche manipulaties om aan te tonen dat de formule a² + b² = c² altijd waar is voor een rechthoekige driehoek.
Er zijn ook meetkundige en trigonometrische bewijzen, waarbij meer gevorderde concepten worden gebruikt om de stelling van Pythagoras te bewijzen.
Waarom is de stelling van Pythagoras belangrijk?
De stelling van Pythagoras is van fundamenteel belang in de wiskunde en heeft vele toepassingen in andere wetenschappelijke gebieden. Het biedt een basis voor het begrijpen van meetkunde, trigonometrie en andere takken van de wiskunde.
Daarnaast heeft de stelling praktische toepassingen. Bijvoorbeeld in de architectuur, waar het helpt bij het berekenen van de afstanden en afmetingen van gebouwen. Ook in de techniek wordt de stelling vaak gebruikt bij het ontwerpen van bruggen, wegen en andere constructies.
Daarnaast heeft de stelling van Pythagoras historische en culturele betekenis. Het werd ontdekt door de oude Griekse wiskundige Pythagoras, die wordt beschouwd als een van de grondleggers van de wiskunde.
Toepassingen van de stelling van Pythagoras
De stelling van Pythagoras heeft vele toepassingen in het dagelijks leven en in verschillende vakgebieden. Enkele voorbeelden zijn:
1. Stelling van Pythagoras voorbeeld: Stel dat we de lengtes van de twee rechthoekszijden van een driehoek kennen. We kunnen de lengte van de schuine zijde vinden door de stelling van Pythagoras toe te passen.
2. Stelling van Pythagoras hoek berekenen: Met behulp van de stelling van Pythagoras kunnen we de hoeken van een rechthoekige driehoek berekenen. Door de verhouding van de zijden te kennen, kunnen we de sinus, cosinus en tangens berekenen.
3. Stelling van Pythagoras calculator: Er zijn vele online tools en rekenmachines beschikbaar die de stelling van Pythagoras automatisch berekenen op basis van de gegeven zijden.
4. Stelling van Pythagoras met 2 onbekenden: Als we twee zijden van een rechthoekige driehoek kennen, kunnen we de derde zijde berekenen met behulp van de stelling van Pythagoras. Dit is nuttig bij het oplossen van meetkundige problemen waarbij verschillende maten betrokken zijn.
5. Stelling van Pythagoras online: Er zijn verschillende online bronnen beschikbaar waar je meer kunt leren over de stelling van Pythagoras, zoals artikelen, video’s en interactieve oefeningen.
6. Omgekeerde stelling van Pythagoras: Deze stelling stelt dat als de zijden van een driehoek aan de stelling van Pythagoras voldoen, de driehoek rechthoekig is. Dit kan worden gebruikt om te controleren of een driehoek rechthoekig is zonder de hoeken te meten.
Kortom, de stelling van Pythagoras is een essentieel concept in de wiskunde met vele praktische toepassingen. Het helpt bij het berekenen van lengtes, afstanden en hoeken in rechthoekige driehoeken en heeft brede toepassingen in verschillende vakgebieden.
Categories: Verzamelen 31 Hoe Werkt Stelling Van Pythagoras
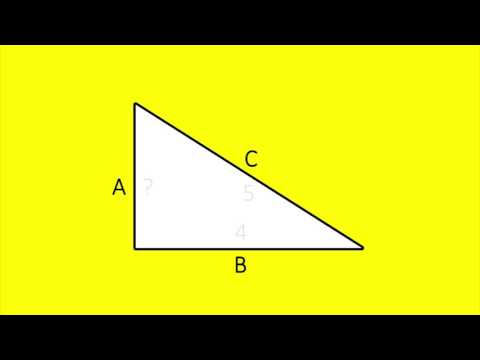
Bij de stelling van Pythagoras kan je de schuine zijde berekenen wanneer je de 2 rechthoekszijden weet. De stelling wordt vaak aangegeven als a2 + b2 = c2. Hierin zijn a en b de rechthoekszijden en c de schuine zijde.We weten wel dat hij een filosoof en een wiskundige was. Ook al was de stelling al langer bekend, Pythagoras was degene die erover schreef en de stelling bewees. Daarom spreken we over de stelling van Pythagoras.De stelling van Pythagoras stelt dat in een rechthoekige drie- hoek de som a² + b² van de kwadraten van de lengtes a en b van rechthoekszijden gelijk is aan het kwadraat van de lengte c van de schuine zijde: a² + b² = c².
Wie Bewees Stelling Van Pythagoras?
Wie Bedacht De Wiskundige Stelling A2 En B2 Is C2?
Hoe Bereken Je Een Hoek Van 90 Graden?
Als je alle zijden van de driehoek weet, maar niet zeker weet of een hoek precies 90 graden is, dan kan je dat controleren met behulp van de stelling van Pythagoras. Deze stelling houdt in dat in een rechthoekige driehoek de som van de kwadraten van de lengtes van de rechthoekszijden gelijk is aan het kwadraat van de lengte van de schuine zijde. Als je dus de formule a² + b² = c² kunt toepassen op de zijden van de driehoek en deze vergelijking klopt, dan heb je aangetoond dat de hoek inderdaad een rechte hoek van 90 graden is.
Verzamelen 27 hoe werkt stelling van pythagoras




See more here: toplist.brokengroundgame.com
Learn more about the topic hoe werkt stelling van pythagoras.
- Hoe Werkt de Stelling van Pythagoras? (Uitleg + Voorbeelden)
- De stelling van Pythagoras: Definitie, formule en uitleg – BijlesHuis blog
- Pythagoras ISBACK – KU Leuven
- Stelling van Pythagoras: hoe werkt het? – Mr. Chadd Academy
- Omgekeerde Stelling van Pythagoras – YouTube
- hoe werkt de stelling van pytagoras | StudyGo
See more: blog https://toplist.brokengroundgame.com/category/opmerkelijk